이진 탐색 트리(Binary Search Tree)

이진 탐색 트리(Binary Search Tree) 란?

이진 탐색 트리 는 이진 트리(Binary Tree) 기반의 탐색을 위한 자료구조 입니다.

이진 탐색 트리 특징

이진 탐색 트리는 다음 4개의 특징을 가지고 있습니다.

모든 노드는 Unique 합니다. 즉 중복된 데이터가 없다는 의미입니다.
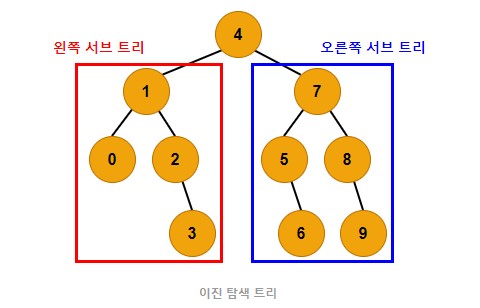
루트 노드를 기준으로 왼쪽 서브 트리 는 루트 노드 보다 작은 값 이 위치 합니다.
루트 노드를 기준으로 오른쪽 서브 트리 는 루트 노드 보다 큰 값 이 위치 합니다.
왼쪽, 오른쪽 서브 트리 또한 이진 탐색 트리입니다.

이진 탐색 트리 구현

노드 삽입
노드 탐색
- 최댓값
- 최솟값
노드 삭제
트리 출력(중위 순회)

이진 탐색 트리의 기본 형태 는 다음과 같습니다.

#include <bits/stdc++.h>
using namespace std;
struct Node {
    int data;
    Node* left;
    Node* right;
    Node(int data) {
        this->data = data;
        this->left = nullptr;
        this->right = nullptr;
    }
};
struct BinarySearchTree {
    Node* root;
    BinarySearchTree() {
        root = nullptr;
    }
    //노드 삽입
    ...
    //노드 탐색
    ...
    //노드 삭제
    ...
    //노드 출력
    ...
};

void solve() {
    BinarySearchTree* bst = new BinarySearchTree();
    ...
}
int main() {
    cin.tie(nullptr);
    ios::sync_with_stdio(false);
    solve();
    return 0;
}

삽입

//노드 삽입
void insertNode(int data) {
    root = insertBST(root, data);
}
Node* insertBST(Node* root, int data) {
    if(root == nullptr) {
        root = new Node(data);
    } else if(root->data > data) {
        root->left = insertBST(root->left, data);
    } else {
        root->right = insertBST(root->right, data);
    }
    return root;
}

탐색

//노드 탐색
bool searchNode(int data) {
    return searchBST(root, data) ? true : false;
}
Node* searchBST(Node* root, int data) {
    if(root == nullptr) {
        return nullptr;
    } else if(root->data == data) {
        return root;
    } else if(root->data > data) {
        return searchBST(root->left, data);
    } else {
        return searchBST(root->right, data);
    }
}
Node* searchMaxNode(Node* root) {
    if(root->right == nullptr) {
        return root;
    } else {
        return searchMaxNode(root->right);
    }
}
Node* searchMinNode(Node* root) {
    if(root->left == nullptr) {
        return root;
    } else {
        return searchMinNode(root->left);
    }
}

삭제

노드가 삭제되어도 이진 탐색 트리는 유지 되어야 하기 떄문에 고려해야할 부분이 있습니다.

삭제한 노드의 자식이 없는 경우
삭제할 노드의 자식이 하나인 경우
삭제한 노드의 자식이 둘인 경우

이때 자식이 둘인 경우 두 가지 방법이 있습니다.

삭제할 노드 기준으로 왼쪽 서브 트리에서 최댓값을 찾고 삭제할 노드의 부모노드와 연결
삭제할 노드 기준으로 오른쪽 서브 트리에서 최솟값을 찾고 삭제할 노드의 부모노드와 연결

위와 같이 부모노드와 삭제될 노드의 자식 노드와 연결 해주어야 합니다. 이진 탐색 트리의 특성에서 보았듯이 이진 탐색 트리의 오른쪽 서브 트리는 루트 노드 보다 큰 값이 오는 특징을 활용 한 것 입니다. 추가로 필자는 위 두가지 중 첫 번째 방법을 사용하여 구현하였습니다.

//노드 삭제
void deleteNode(int data) {
    if(root != nullptr) {
        root = deleteBST(root, data);
    } else {
        return;
    }
}
Node* deleteBST(Node* root, int data) {
    if(root->data > data) {
        root->left = deleteBST(root->left, data);
    } else if(root->data < data) {
        root->right = deleteBST(root->right, data);
    } else {
        Node* tmp = root;
        //자식이 없을때
        if(root->left == nullptr && root->right == nullptr) {
            root = nullptr;
            delete tmp;
        } //자식이 하나일때
        else if(root->left == nullptr) {
            root = root->right;
            delete tmp;
        } else if(root->right == nullptr) {
            root = root->left;
            delete tmp;
        //자식이 두명일때 왼쪽 노드중 가장 큰값 연결 
        } else {
            tmp = searchMaxNode(root->left);
            root->data = tmp->data;
            root->left = deleteBST(root->left, tmp->data);
        }
    }
    return root;
}

전체 코드

#include <bits/stdc++.h>
using namespace std;
struct Node {
    int data;
    Node* left;
    Node* right;
    Node(int data) {
        this->data = data;
        this->left = nullptr;
        this->right = nullptr;
    }
};
struct BinarySearchTree {
    Node* root;
    BinarySearchTree() {
        root = nullptr;
    }
    //노드 삽입
    void insertNode(int data) {
        root = insertBST(root, data);
    }
    Node* insertBST(Node* root, int data) {
        if(root == nullptr) {
            root = new Node(data);
        } else if(root->data > data) {
            root->left = insertBST(root->left, data);
        } else {
            root->right = insertBST(root->right, data);
        }
        return root;
    }
    //노드 탐색
    bool searchNode(int data) {
        return searchBST(root, data) ? true : false;
    }
    Node* searchBST(Node* root, int data) {
        if(root == nullptr) {
            return nullptr;
        } else if(root->data == data) {
            return root;
        } else if(root->data > data) {
            return searchBST(root->left, data);
        } else {
            return searchBST(root->right, data);
        }
    }
    Node* searchMaxNode(Node* root) {
        if(root->right == nullptr) {
            return root;
        } else {
            return searchMaxNode(root->right);
        }
    }
    Node* searchMinNode(Node* root) {
        if(root->left == nullptr) {
            return root;
        } else {
            return searchMinNode(root->left);
        }
    }
    //노드 삭제
    void deleteNode(int data) {
        if(root != nullptr) {
            root = deleteBST(root, data);
        } else {
            return;
        }
    }
    Node* deleteBST(Node* root, int data) {
        if(root->data > data) {
            root->left = deleteBST(root->left, data);
        } else if(root->data < data) {
            root->right = deleteBST(root->right, data);
        } else {
            Node* tmp = root;
            //자식이 없을때
            if(root->left == nullptr && root->right == nullptr) {
                root = nullptr;
                delete tmp;
            } //자식이 하나일때
            else if(root->left == nullptr) {
                root = root->right;
                delete tmp;
            } else if(root->right == nullptr) {
                root = root->left;
                delete tmp;
            //자식이 두명일때 왼쪽 노드중 가장 큰값 연결 
            } else {
                tmp = searchMaxNode(root->left);
                root->data = tmp->data;
                root->left = deleteBST(root->left, tmp->data);
            }
        }
        return root;
    }
    //노드 출력
    void printTree(Node* root) {
        if(root == nullptr) return;
        printTree(root->left);
        cout << root->data << " ";
        printTree(root->right);
    }
};

void solve() {
    BinarySearchTree* bst = new BinarySearchTree();
    bst->insertNode(4);
    bst->insertNode(2);
    bst->insertNode(1);
    bst->insertNode(3);
    bst->insertNode(6);
    bst->insertNode(5);
    bst->insertNode(7);
    /*
          4
        /  \
       2    6
      / \  / \
     1  3 5   7 */
    bst->printTree(bst->root);
    cout << "\n";
    bst->deleteNode(5);
    bst->deleteNode(6);
    bst->deleteNode(2);
    bst->printTree(bst->root);
    cout << "\n";
    /*
          4
        /  \
       3    7
      /    
     1  */
     cout << bst->searchNode(3) << "\n"; // true
     cout << bst->searchNode(5) << "\n"; // false
}

int main() {
    cin.tie(nullptr);
    ios::sync_with_stdio(false);
    solve();
    return 0;
}

이진 탐색 트리의 삽입, 삭제, 검색 시간복잡도는
평균: O(logN), 최악: O(N) 입니다.

이진 탐색 트리 활용1

오름차순으로 정렬된 배열을 이진 검색 트리로 만들기

#include <bits/stdc++.h>
using namespace std;
struct Node {
    int data;
    Node* left;
    Node* right;
    Node(int data) {
        this->data = data;
    }
};
Node* makeTree(int arr[], int start, int end) {
    if(start > end) return NULL;
    int mid = (start + end) / 2;
    Node* node = new Node(arr[mid]);
    node->left = makeTree(arr, start, mid-1);
    node->right = makeTree(arr, mid+1, end);
    return node;
}

void searchTree(Node* root) {
    if(root == NULL) return;
    cout << root->data << " ";
    searchTree(root->left);
    searchTree(root->right);
}
void solve() {
    int arr[10] = {0,1,2,3,4,5,6,7,8,9};
    Node* root;
    root = makeTree(arr, 0, 9);
    searchTree(root);
}

int main() {
    cin.tie(nullptr);
    ios::sync_with_stdio(false);
    solve();
    return 0;
}

record

DataStructure