다익스트라 알고리즘(Dijkstra Algorithm) 이란?
- 다익스트라 알고리즘(Dijkstra Algorithm)은 다이나믹 프로그래밍 을 활용한 대표적인 최단 경로 탐색 알고리즘 이다. 흔히 인공위성, GPS 소프트웨어 등에서 많이 사용된다.
다익스트라 알고리즘(Dijkstra Algorithm)의 특징
- 다익스트라 알고리즘은 하나의 정점 에서 다른 모든 정점 들의 최단 경로 를 구하는 알고리즘이다.
( single source shortest path problem )
다익스트라 알고리즘(Dijkstra Algorithm)의 알고리즘 예시
- 출발 노드를 설정한다.
- 출발 노드를 기준으로 각 노드의 최소 비용을 저장한다.
- 방문하지 않은 노드 중에서 가장 비용이 적은 노드를 선택한다.
- 해당 노드를 거쳐서 특정한 노드로 가는 경우를 고려하여 최소 비용을 갱신한다.
- 3 ~ 4 과정을 반복한다.
( single source shortest path problem )
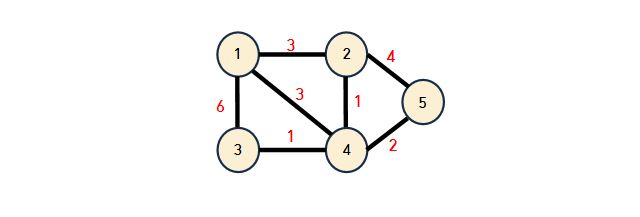
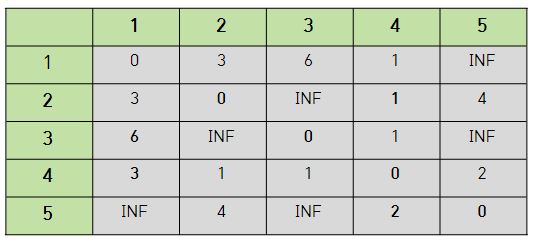
다음과 같은 그래프는 실제로 컴퓨터 안에서 처리할 때 이차원 배열 형태로 처리해야 한다.
- 특정 행에서 열로 가는 비용 표
위의 표를 보면 1행 2열의 값이 3인것을 알 수 있다. 이는 위의 그래프에서 노드1에서 노드2로 가는 비용을 의미한다.
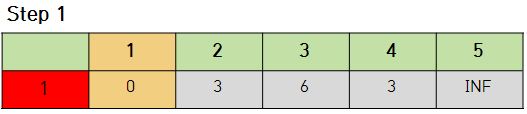
- 1번 노드를 선택했을 경우
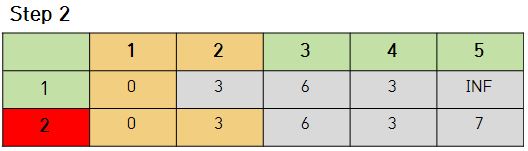
- 2번 노드를 선택했을 경우
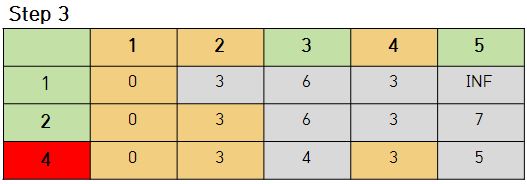
2번 노드를 선택했을 때 2번 노드에서 5번 노드로 가는 비용이 이전 값인 무한대 보다 작기 때문에 7로 갱신됨을 알 수 있다.
그리고 가장 작은 비용인 3(4번 노드)을 선택한다.
- 4번 노드를 선택했을 경우
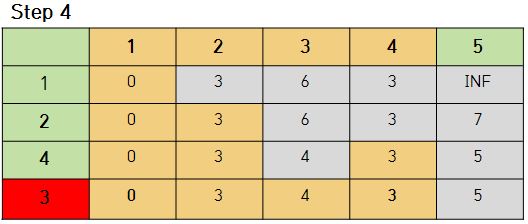
4번 노드를 선택했을때 3번 노드로 가는 비용이 이전에 1번 노드에서 3번 노드로 가는 비용보다 4번 노드를 거쳐서 가는 비용이 더 적기 때문에 4로 갱신해준다.
또한 5번 노드로 가는 비용 또한 4번 노드를 거쳐가는 것이 Step2에서 2번 노드를 선택했을때 갱신했던 비용보다 더 적기 때문에 새롭게 갱신해준다.
- 3번 노드를 선택했을 경우
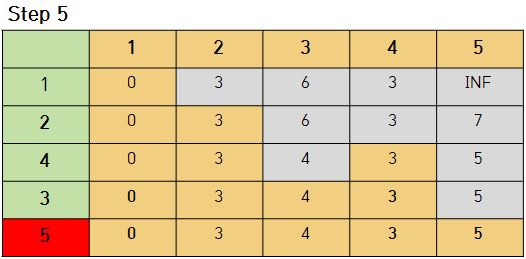
- 5번 노드를 선택했을 경우
- 결과적으로 1번 노드에서 출발하여 각 노드로 가는 최소 비용 은 0 3 4 3 5 가 된다.
선형 탐색을 이용한 다익스트라 알고리즘(Dijkstra Algorithm) 구현
- 정점의 갯수는 많은 데 간선은 적을 때 치명적일 정도로 비효율적으로 작동할 수 있다.
선형 탐색 으로 찾는 경우 시간 복잡도가 O(N^2) 이다.
#include <stdio.h>
int num = 6;
// 무한을 표현하려고 선언
int INF = 1000000000;
// 전체 그래프 초기화
int a[6][6] = {
{0, 2, 5, 1, INF, INF},
{2, 2, 5, 1, INF, INF},
{5, 3, 0, 3, 1, 5},
{1, 2, 3, 0, 1, INF},
{INF, INF, 1, 1, 0, 2},
{INF, INF, 5, INF, 2, 0},
};
bool v[6]; // 방문한 노드인지 확인 배열
int d[6]; // 최단거리
// 가장 최소 거리를 가지는 정점을 반환한다.
// 시간 복잡도 O(N)
int getSmallIndex(){
int min = INF;
int index = 0;
for(int i = 0; i < num; i++) {
if(d[i] < min && !v[i]){
min = d[i];
index = i;
}
}
return index;
}
void dijkstra(int start){
for(int i = 0; i < num; i++){
d[i] = a[start][i];
}
v[start] = true;
for(int i =0; i < num - 2; i++){
int current = getSmallIndex();
v[current] = true;
// 시간 복잡도 O(N)
for(int j = 0; j < 6; j++){
// 방문하지 않았다면
if(!v[j]){
// 현재 보고있는 노드의 최소비용에서 해당 노드를 거처서 그 노드의 인접한 노드로 가는 비용을 더한 값
// 현재 인접한 노드로 가는 최소 비용보다 더 작다면 갱신해준다.
if( d[current] + a[current][j] < d[j] ) {
d[j] = d[current] + a[current][j];
}
}
}
}
}
int main(void) {
dijkstra(0);
for(int i = 0; i < num; i++) {
printf("%d ", d[i]);
}
return 0;
}인접 리스트 방식을 이용한 다익스트라 알고리즘(Dijkstra Algorithm) 구현
- 정점에 비해 간선의 갯수가 비정상적으로 적어도 안정적으로 처리할 수 있다.
- 실제 알고리즘 대회에서 인접 리스트를 이용한 방식으로 많이 구현한다.
- 힙(Heap)을 이용한 경우 가장 작은 값을 가져오는 과정(getSmallIndex())을 logN 만큼 으로 줄일 수 있다.
따라서, 인접 리스트 방식을 이용한 경우 시간 복잡도가 O(N * logN) 이다.
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
int num = 6;
// 무한을 표현하려고 선언
int INF = 1000000000;
vector<pair<int, int> > a[7]; // 간선 정보
int d[7]; // 최단거리 (최소 비용)
void dijkstra(int start){
d[start] = 0;
// priority_queue는 기본적으로 더 큰값을 기준으로 최상단 노드를 만든다. (최대 힙)
priority_queue<pair<int, int> > pq; // 힙 구조 입니다.
pq.push(make_pair(start, 0));
// 가까운 순서대로 처리하므로 큐를 사용한다.
// priority_queue 가 비어있지 않다면 하나씩 꺼낸다.
while(!pq.empty()) {
int current = pq.top().first;
// priority_queue가 최대힙 구조로 형성이 되기때문에
// 짧은 것이 먼저 오도록 음수화(-) 한다.
int distance = -pq.top().second;
pq.pop();
// 최단 거리가 아닌 경우 스킵
if(d[current] < distance) continue;
for(int i = 0; i < a[current].size(); i++) {
// 선택된 노드의 인접 노드
int next = a[current][i].first;
// 선택된 노드 거쳐서 인접 노드로 가는 비용
int nextDistance = distance + a[current][i].second;
// 기존의 최소 비용보다 더 저렴하다면 교체한다.
if(nextDistance < d[next]) {
d[next] = nextDistance;
// nextDistance를 음수로 저장하는 이유 힙이 최대 힙 구조로 형성되기 때문이다.
// 더 작은 값이 윗 쪽으로 가게 만들기 위해서이다.
pq.push(make_pair(next, -nextDistance));
}
}
}
}
int main(void) {
// 연결되지 않은 경우 비용은 무한
for(int i = 1; i <= num; i++) {
d[i] = INF;
}
a[1].push_back(make_pair(2, 2));
a[1].push_back(make_pair(3, 5));
a[1].push_back(make_pair(4, 1));
a[2].push_back(make_pair(1, 2));
a[2].push_back(make_pair(3, 3));
a[2].push_back(make_pair(4, 2));
a[3].push_back(make_pair(1, 5));
a[3].push_back(make_pair(2, 3));
a[3].push_back(make_pair(4, 3));
a[3].push_back(make_pair(5, 1));
a[3].push_back(make_pair(6, 5));
a[4].push_back(make_pair(1, 1));
a[4].push_back(make_pair(2, 2));
a[4].push_back(make_pair(3, 3));
a[4].push_back(make_pair(5, 1));
a[5].push_back(make_pair(3, 1));
a[5].push_back(make_pair(4, 1));
a[5].push_back(make_pair(6, 2));
a[6].push_back(make_pair(3, 5));
a[6].push_back(make_pair(5, 2));
dijkstra(1);
// 결과 출력
for(int i = 1; i <= num; i++) {
printf("%d ", d[i]);
}
return 0;
} 다익스트라 구현(java)
import java.util.HashMap;
import java.util.*;
class Destination implements Comparable<Destination> {
String destination;
int distance;
int time;
Destination(String destination, int distance, int time) {
this.destination = destination;
this.distance = distance;
this.time = time;
}
@Override
public int compareTo(Destination o) {
return this.distance <= o.distance ? 1 : -1;
}
}
public class Dijkstra {
static String[] initVertex = {"교대역","강남역","남부터미널역",
"양재역","매봉역","역삼역","양재시민의숲역"};
static Map<String, List<Destination> > map = new HashMap<>();
static Map<String, Integer> check = new HashMap<>();
public static void dijkstra(String start, String end) {
PriorityQueue<Destination> pq = new PriorityQueue<>();
pq.add(new Destination(start, 0, 0));
while (!pq.isEmpty()) {
Destination cur = pq.poll();
String curPosition = cur.destination;
int curDist = -cur.distance;
int curTime = cur.time;
if (curPosition == end) {
System.out.println("거리: "+curDist+"km\n시간: "+curTime+"초");
return;
}
if (!map.containsKey(curPosition)) continue;
if (check.get(curPosition) < curDist) continue;
for (int i = 0; i < map.get(curPosition).size(); i++) {
Destination next = map.get(curPosition).get(i);
String nextPosition = next.destination;
int nextDist = curDist + next.distance;
int nextTime = curTime + next.time;
if (check.get(nextPosition) > nextDist) {
check.put(nextPosition, nextDist);
pq.add(new Destination(nextPosition, -nextDist, nextTime));
}
}
}
}
public static void init() {
map.computeIfAbsent("교대역", V->new ArrayList<>()).add(new Destination("강남역", 2, 3));
map.computeIfAbsent("강남역", V->new ArrayList<>()).add(new Destination("역삼역", 2, 3));
map.computeIfAbsent("교대역", V->new ArrayList<>()).add(new Destination("남부터미널역", 3, 2));
map.computeIfAbsent("남부터미널역", V->new ArrayList<>()).add(new Destination("양재역", 6, 5));
map.computeIfAbsent("양재역", V->new ArrayList<>()).add(new Destination("매봉역", 1, 1));
map.computeIfAbsent("강남역", V->new ArrayList<>()).add(new Destination("양재역", 2, 8));
map.computeIfAbsent("양재역", V->new ArrayList<>()).add(new Destination("양재시민의숲역", 10, 3));
for (String vertex : initVertex) {
check.put(vertex, 9999);
}
}
public static void main(String[] args) {
init();
dijkstra("교대역", "양재역");
}
}