이분 매칭(Bipartite Matching) 이란?
- 네트워크 플로우 의 개념중에서 이분 그래프(Bipartite Graph) 에서의 최대 유량을 구하는 경우를 이분 매칭 이라고 부른다.
- 이분 매칭(Bipartite Matching)은 A집단이 B집단을 선택하는 방법에 대한 알고리즘이다.
이분 매칭(Bipartite Matching) 알고리즘의 특징
- A집단이 B집단을 선택할때 효과적으로 매칭시켜준다는 점에서 ‘최대 매칭(Max Matching)’ 을 의미한다.
- 깊이 우선 탐색(DFS) 으로 이분 매칭을 풀면 빠르고 효율적인 알고리즘을 설계할 수 있다.
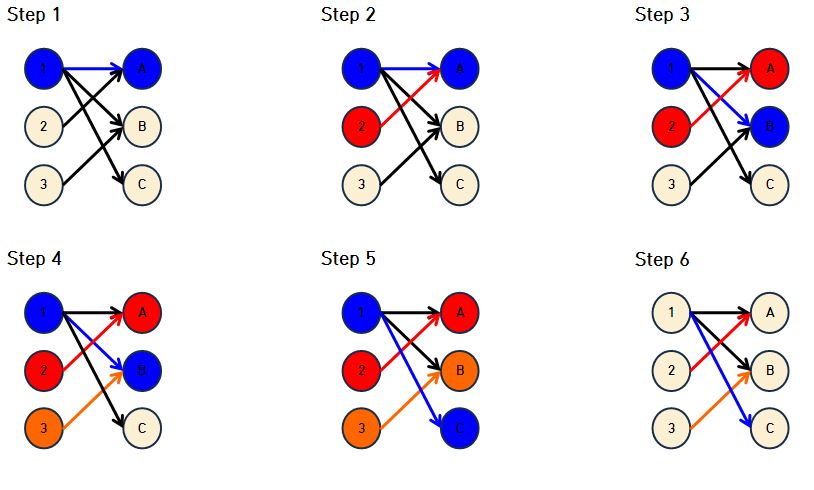
이분 매칭(Bipartite Matching)의 알고리즘 예시
- 이분 그래프의 이분 매칭 과정.
- Step 1. 정점 1은 아무것도 선택되지 않은 정점 A를 선택한다.
- Step 2. 정점 2는 선택할 수 있는 정점이 정점 A 밖에 존재하지 않는다. 그러나 이미 정점 1이 점유 하고 있다. 이러한 상황에서 정점 A를 점유 하고있는 정점 1에서부터 다시 출발하여, A를 제외하고 다른 곳으로 연결될 수 있는지 확인한다.
- Step 3. 확인 결과, 정점 1은 B와 연결이 가능하므로 정점 B에 연결한다.
- Step 4. 정점 3도 동일하게 선택할 수 있는 정점이 정점 B 밖에 없는데 정점 B를 정점 A가 점유 하고 있으므로 다시 정점 A에서 부터 출발하여 다른 곳으로 연결될 정점을 확인한다.
- Step 5. 확인 결과, 정점 1은 정점 C에 연결이 된다.
- Step 6. 최종적으로 1 - C, 2 - A, 3 - B로 최대로 매칭 됨을 확인할 수 있다.
Source Code
#include <iostream>
#include <vector>
#define MAX 101
using namespace std;
vector<int> a[MAX]; // 각 정점과 연결된 간선 정보
int d[MAX]; // 점유 하고있는 노드의 정보
bool c[MAX]; // 특정 정점을 처리했는지 여부
int n = 3, m; // m 간선의 개수
// 매칭에 성공한 경우 True, 실패한경우 false
bool dfs(int x) {
// 연결된 모든 노드에 대해서 들어갈 수 있는 시도
for(int i = 0; i < a[x].size(); i++){
int t = a[x][i];
// 이미 처리한 노드는 더 이상 볼 필요가 없음
if(c[t]) continue;
c[t] = true;
// 비어있거나 점유 노드에 더 들어갈 공간이 있는 경우
if(d[t] == 0 || dfs(d[t])){
d[t] = x;
return true;
}
}
return false;
}
int main(void) {
a[1].push_back(1);
a[1].push_back(2);
a[1].push_back(3);
a[2].push_back(1);
a[3].push_back(2);
int count = 0;
for(int i = 1; i <= n; i++){
fill(c, c + MAX, false);
if(dfs(i)) count++;
}
printf("%d 개의 매칭이 이루어졌습니다. \n", count);
for(int i = 1; i < MAX; i++){
if(d[i] != 0) {
printf("%d -> %d \n", d[i], i);
}
}
return 0;
}이분 매칭(Bipartite Matching)의 시간복잡도
깊이 우선 탐색(DFS)를 이용해 이분 매칭을 간단히 풀 때
시간 복잡도는 O(V * E) 이다. 이 방법은 가장 빠른 속도의 알고리즘은 아니지만 구현이 가장 간단하고 쉽다는 점에서 많이 사용된다.