record

합집합 찾기(Union-Find) 이란?

• 합집합 찾기(Union-Find)는 대표적인 그래프 알고리즘 이다. 서로소 집합(Disjoint-Set) 알고리즘 이라고도 부른다.
• 합집합 찾기(Union-Find)는 Disjoint Set을 표현할 때 사용하는 알고리즘이다.
  • Disjoint Set을 구현하는 데 트리, 비트 벡터, 배열, 연결 리스트를 이용할 수 있다.
• 합집합 찾기(Union-Find)는 여러 개의 노드가 존재할 때 두 개의 노드를 선택해서, 현재 이 두 노드가 서로 같은 그래프에 속하는지 판별 하는 알고리즘이다.

합집합 찾기(Union-Find)의 특징

• 집합 을 구현하는데에 있어서 비트 벡터, 배열, 연결 리스트 보다 트리를 이용한 방법이 가장 효율적이다.
• 합집합 찾기(Union-Find)의 연산
  • Find() : 어떤 원소가 주어졌을 때 이 원소가 속한 집합을 반환.
  • Union() : 두 개의 집합을 하나의 집합으로 합친다.

트리를 이용한 방법으로 구현하는 이유

배열을 이용하여 Union-Find를 구현 할 수 있지만, Union 연산 수행 시 배열의 모든 원소를 순회해야 하기 때문에 시간복잡도가 O(N) 이 된다.

• 트리를 이용하여 Union-Find를 구현하면 배열보다 빠르게 Union 연산을 수행할 수 있다.

합집합 찾기(Union-Find)의 알고리즘 예시

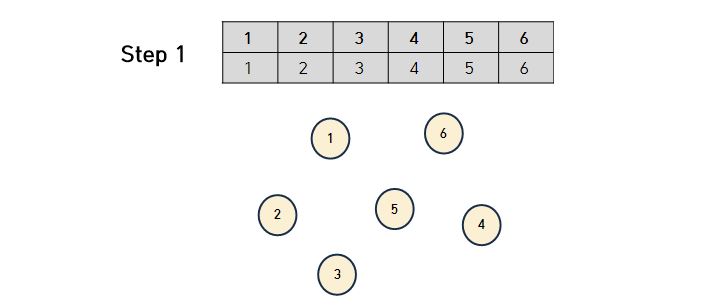
• Step 1과 같이 여러개의 노드가 연결되지 않고 존재한다고 하자. 그리고 배열에 모든 값이 각자 자기 자신을 가리키도록 만든다. 배열의 첫 번째 행은 ‘노드 번호’를 의미하고 두 번째 행은 ‘부모 노드 번호’를 의미한다. 즉, 자기 자신이 어떠한 부모에 포함되어 있는지를 의미한다.

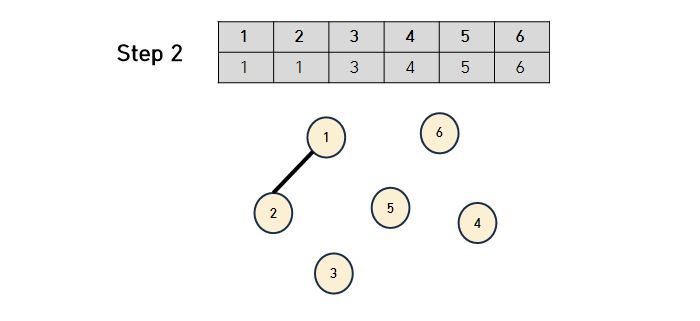
• Step 2와 같이 1과 2가 연결되었을때 2번 노드의 두 번째 행인 부모 노드 번호가 ‘1’ 이 들어간다. 이렇게 부모를 합칠 때는 일반적으로 더 작은 값 쪽으로 합친다. 이것을 Union 이라고 한다.

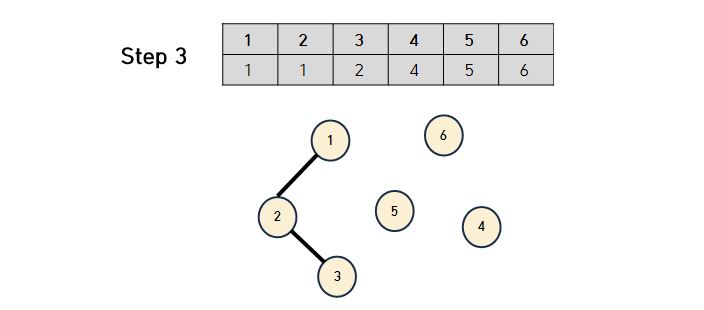
• Step 3에서 2와 3이 연결이 된다면 3번의 부모 노드 번호는 2가 된다. 그러나 여기서 중요한 점은 ‘1과 3이 연결되었는지는 어떻게 파악할 수 있는가’ 이다. 1과 3의 부모가 각각 1과 2로 다르기 때문에 ‘부모 노드’만 보고는 한번에 파악할 수 없다. 그렇기 때문에 재귀 함수가 사용된다.

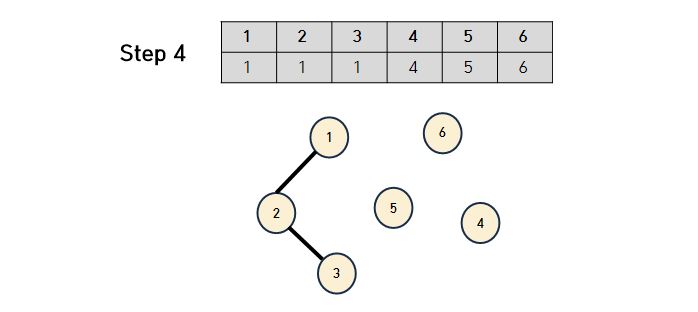
• Step 4와 같이 3의 부모를 찾기 위해서는 먼저 3이 가리키고 있는 2를 찾는다. 그러면 2의 부모가 1을 가리키고 있으므로 결과적으로 3의 부모는 1이 되는것을 파악할 수 있는 것이다.
• 이러한 과정은 재귀적으로 수행될 때 가장 효과적이고 직관적으로 작성할 수 있다.

C++ STL Library를 사용한 합집합 찾기(Union-Find) 구현

#include <stdio.h>

// 부모 노드를 찾는 함수 
int getParent(int parent[], int x) {
	if(parent[x] == x) return x;
	return parent[x] = getParent(parent, parent[x]);
} 
// 두 부모 노드를 합치는 함수 
int unionParent(int parent[],int a, int b){
	a = getParent(parent, a);
	b = getParent(parent, b);
	if(a < b) parent[b] = a;
	else parent[a] = b;
	
}

// 같은 부모를 가지는지 확인 == 같은 그래프인지 확인 
int findParent(int parent[], int a, int b){
	a = getParent(parent, a);
	b = getParent(parent, b);
	if(a == b) return 1;
	return 0;
}

int main(void){
	int parent[11];
	for(int i = 0; i <= 10; i++){
		parent[i] = i;
	}
	unionParent(parent, 1, 2);
	unionParent(parent, 2, 3);
	unionParent(parent, 3, 4);
	unionParent(parent, 5, 6);
	unionParent(parent, 6, 7);
	unionParent(parent, 7, 8);
	
	printf("1과 5가 연결되어있나? %d \n", findParent(parent, 1, 5));
	unionParent(parent, 1, 5);
	printf("1과 5가 연결되어있나? %d \n", findParent(parent, 1, 5));
	
	return 0;
}

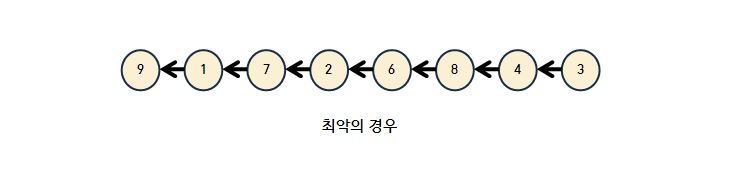
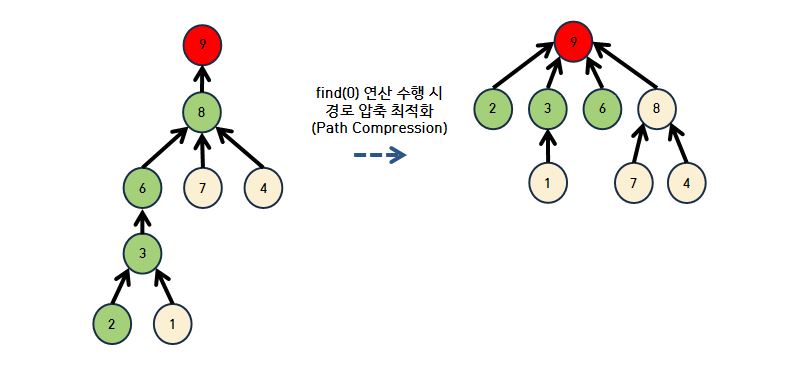
Union-Find 최악의 경우 & 최적화한 방법

최악의 상황

• 트리 구조가 완전 비대칭인 경우
• 연결 리스트 형태인 경우
• 트리의 높이가 최대가 되는 경우

  원소의 개수가 N일 때, 트리의 높이가 N-1이므로 union과 find(x)의 시간 복잡도가 모두 O(N)이 된다. 배열로 구현하는 것보다 비효율적이다.

find 연산 최적화

References

• 18강 - 합집합 찾기(Union-Find)
• https://bowbowbow.tistory.com/26
• [알고리즘] Union-Find 알고리즘