그래프(Graph)

그래프(Graph)란?

그래프(Graph) 란 현실 세계의 사물이나 추상적인 개념 간의 연결 관계를 표현한것을 말합니다.
그래프(Graph) 는 어떤 자료나 개념을 표현하는 정점(vertex) 들과 이들을 연결하는 간선(edge) 들로 구성된 자료 구조입니다.

그래프(Graph)의 종류와 특징에 대해서 알아보기 전에 그래프의 실생활 예시 를 알아 보겠습니다.

여러 도시들을 연결하는 도로망
사람들간의 지인 관계
웹사이트 간의 링크 관계

그래프는 트리에 있었던 부모 자식 관계에 관한 제약이 없기 때문에 그래프는 트리보다 훨씬 다양한 구조를 표현할 수 있고, 현실 세계의 수많은 문제들을 푸는 데 유용하게 사용됩니다.

그래프 구성요소(용어)

정점(vertex): 위치라는 개념. (node 라고도 부름)
간선(edge): 위치 간의 관계. 즉, 노드를 연결하는 선 (link, branch 라고도 부름)
인접 정점(adjacent vertex): 간선에 의 해 직접 연결된 정점
정점의 차수(degree): 무방향 그래프에서 하나의 정점에 인접한 정점의 수
- 무방향 그래프에 존재하는 정점의 모든 차수의 합 = 그래프의 간선 수의 2배
진입 차수(in-degree): 방향 그래프에서 외부에서 오는 간선의 수 (내차수 라고도 부름)
진출 차수(out-degree): 방향 그래프에서 외부로 향하는 간선의 수 (외차수 라고도 부름)
- 방향 그래프에 있는 정점의 진입 차수 또는 진출 차수의 합 = 방향 그래프의 간선의 수(내차수 + 외차수)
경로 길이(path length): 경로를 구성하는 데 사용된 간선의 수
단순 경로(simple path): 경로 중에서 반복되는 정점이 없는 경우
사이클(cycle): 단순 경로의 시작 정점과 종료 정점이 동일한 경우

그래프의 특징

그래프는 네트워크 모델 입니다.
2개 이상의 경로가 가능합니다.
- 즉, 정점들 사이에 무방향/방향에서 양방향 경로를 가질 수 있습니다.
1->1(self-loop) 뿐 아니라 반복/순회 모두 가능합니다.
트리와 달리 루트 노드 라는 개념이 없습니다.
- 따라서, 부모-자식 관계라는 개념이 없습니다.
그래프의 탐색(순회)는 DFS 나 BFS 로 이루어집니다.
그래프는 순환(Cyclic) 혹은 비순환(Acyclic) 입니다.
그래프는 크게 방향(=유향) 그래프 와 무방향(=무향) 그래프 가 있습니다.
간선의 유무는 그래프에 따라 다릅니다.

그래프의 종류

datastructure-graph-category

그래프는 여러 가지 변형된 형태를 가질 수 있습니다.

정점 혹은 간선에 추가적인 속성을 부여
형태에 제약을 둘 수 있습니다.

그래프 는 대표적으로 간선에 방향이라는 추가적 속성을 부여하여 크게 유향(=방향, directed) 그래프 와 무향(undirected) 그래프 두가지로 나뉩니다. 또한 가중치라는 속성을 가진 가중치 그래프 가 있습니다.

이외에 다중 그래프, 단순 그래프, 루트 없는 트리 그래프, 이분 그래프, 사이클 없는 방향 그래프(DAG) 등이 있습니다.

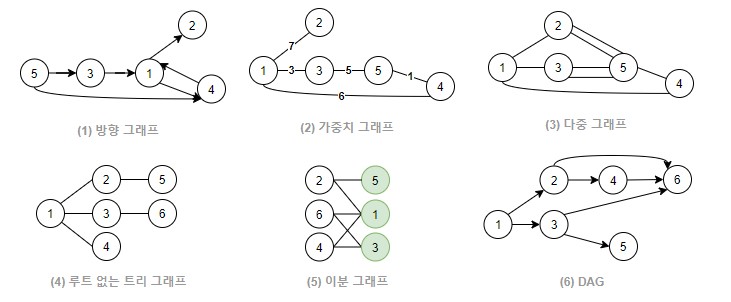
유향(=방향, directed) 그래프
- 그림(1)과 같이 그래프의 각 간선이 방향 이라는 새로운 속성을 갖습니다.
무향(undirected) 그래프
- 간선에 방향이 없는 그래프를 말합니다.
가중치(weighted) 그래프
- 그림(2)과 같이 각 간선에 가중치(weighted) 라고 불리는 실수 속성을 부여한 그래프를 말합니다.
- 두 도시 사이의 거리, 두 물건 사이의 교환 비율, 두 사람 사이의 호감도 등의 다양한 정보를 표현하는 데 사용할 수 있습니다.

다음은 그래프의 형태로 그래프를 분류 한 경우입니다.

다중(multi) 그래프
- 그림(3)과 같이 두 정점 사이에 두 개 이상의 간선이 있는 경우.
- 도로망과 같은 두 지점을 잇는 두개 이상의 도로를 표현하는 데 사용할 수 있습니다.
- 단순(simple) 그래프: 두 정점 사이에 최대 한 개의 간선만 있는 그래프
루트 없는 트리 그래프
- 그림(4)와 같이 트리 혹은 루트 없는 트리는 부모 자식 관계가 없을 뿐, 간선들의 연결 관계만 보면 트리와 같은 무향 그래프 를 말합니다.
- 간선들의 연결 관계만 보면 트리와 같다는 말은, 간선을 통해 두 정점을 잇는 방법이 딱 하나밖에 없다는 의미입니다.
이분(bipartite) 그래프
- 그림(5)와 같이 그래프의 정점들을 겹치지 않는 두 개의 그룹으로 나눠서 서로 다른 그룹에 속한 정점들 간에만 간선이 존재하도록 만들 수 있는 그래프를 말합니다.
- 자세한 내용은 이곳을 참고해주세요.
사이클 없는 방향 그래프(DAG)
- 방향 가중치 그래프, 이분 가중치 그래프와 같이 두 가지 속성을 가지고 있는 그래프를 말합니다.
- 그림(6) DAG는 방향 그래프 로 한 점에서 출발해 자기 자신으로 돌아오는 경로(사이클)가 존재하지 않는 경우를 말합니다.
- 여러 작업들간의 상호 의존 관계 등을 표현하는 데 사용할 수 있습니다.

그래프(Graph)와 트리(Tree) 비교

	그래프(Graph)	트리(Tree)
정의	정점(vertex)과 그것을 연결하는 간선(edge)들로 이루어진 자료구조	그래프의 한 종류인 DAG의 한 종류
방향성	방향 그래프, 무방향 그래프 존재	방향 그래프 존재
사이클	사이클, 자체 간선(self-loop), 순환(Cyclic) 비순환(Acyclic) 존재	사이클 절대 불가능
루트 노드	없음	한 개 존재
부모-자식	없음	존재
모델	네트워크 모델	계층 모델
탐색(순회)	DFS, BFS	Pre, In, Post Order
간선의 수	간선이 있을수도 없을수도 있음	노드가 N개인 트리의 간선의 수는 N-1개
경로	-	임의의 두 노드 간의 경로가 유일

그래프 구현 방법

인접 리스트(Adjacency List)
인접 행렬(Adjacency Matrix)

인접 리스트(Adjacency List)

각 정점마다 하나의 연결 리스트 를 갖는 방식입니다.

int n = 10; // 정점의 개수
vector<int> adjacent[n];

adjacent[1].push_back(2);// 1->2
adjacent[1].push_back(3);// 1->3

인접 리스트 는 O(｜V｜+｜E｜) 의 공간을 사용 합니다.

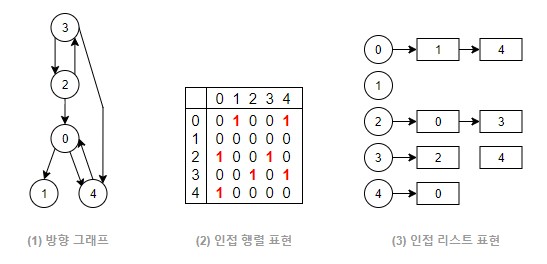
인접 행렬(Adjacency Matrix)

인접 리스트 표현의 큰 단점은 두 정점이 주어질 때 이 정점이 연결되어 있는 지를 알기 위해서 연결리스트를 일일이 뒤져야합니다. 이와 같은 연산의 속도를 높이기 위해 고안된 표현 방식이 인접 행렬(Adjacency Matrix) 로 표현한 방식입니다.

vector<vector<int> > adjacent;
adjacent[1][2] = 1; // 1->2
adjacent[1][3] = 1; // 1->2

인접 행렬 은 간선 개수와 관계없이 항상 O(｜V｜²) 크기의 공간을 사용 합니다.

그래프 구현 방법 비교

datastructure-graph-impl

※참고※
간선의 수가 |V|²에 비해 훨씬 적은 그래프를 희소(sparse) 그래프
반대로 간선의 수가 거의 |V|²에 비례하는 그래프를 밀집(dense) 그래프 라고 합니다.

따라서, 희소 그래프는 인접 리스트를 밀집 그래프는 인접 행렬을 사용하는 것이 유리 합니다.

References

알고리즘 문제 해결 전략(종만북)
gmlwjd9405.github.io/

record

DataStructure