플로이드 와샬 알고리즘(Floyd Warshall Algorithm) 이란?
- ‘모든 정점’ 에서 ‘모든 정점’ 으로의 최단 경로를 구하는 알고리즘.
※참고※
다익스트라 알고리즘은 하나의 정점에서 출발했을 때 다른 모든 정점으로의 최단 경로를 구하는 알고리즘이다.
플로이드 와샬 알고리즘(Floyd Warshall Algorithm)의 특징
- ‘거쳐가는 정점’ 을 기준으로 최단 거리를 구하는 알고리즘을 수행한다.
※참고※
다익스트라 알고리즘은 가장 적은 비용을 하나씩 선택하여 수행한다.
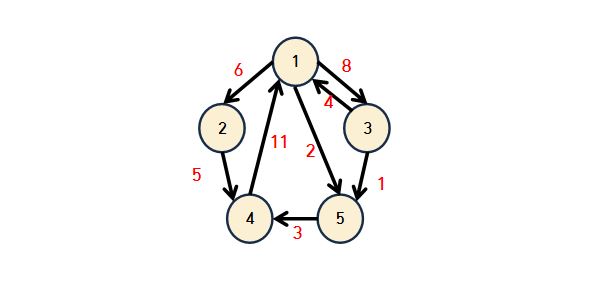
플로이드 와샬 알고리즘(Floyd Warshall Algorithm)의 알고리즘 예시
※참고※
다익스트라 알고리즘은 하나의 정점에서 출발했을 때 다른 모든 정점으로의 최단 경로를 구하는 알고리즘이다.
※참고※
다익스트라 알고리즘은 가장 적은 비용을 하나씩 선택하여 수행한다.
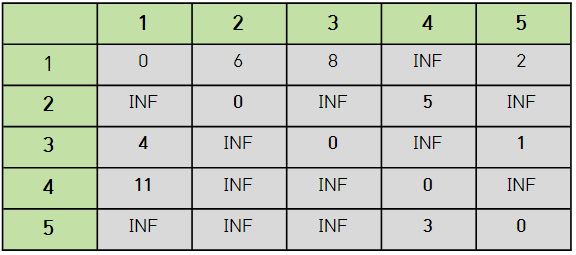
위의 그래프를 이차원 배열의 형태로 출력하면 다음과 같다.
- 현재까지 계산된 최소 비용 테이블
이 테이블은 ‘현재까지 계산된 최소 비용’ 을 의미한다. 이러한 이차원 배열을 반복적으로 갱신하여 최종적으로 모든 최소비용을 구하면 된다. 바로 그러한 반복의 기준이 ‘거쳐가는 정점’ 인 것이다.
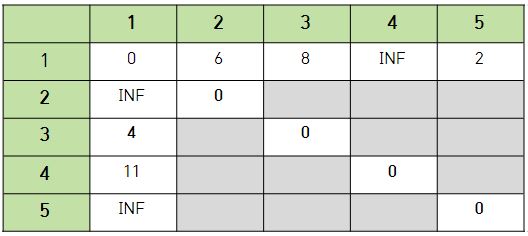
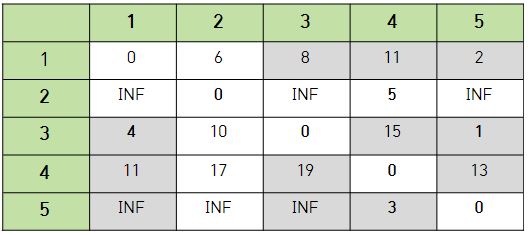
- 노드 1을 거쳐가는 경우
노드 1을 거쳐가는 경우 회색으로 칠해진 12개의 공간만을 갱신해주면된다.
X에서 Y로 가는 최소 비용 VS X에서 노드 1로 가는 비용 + 노드 1에서 Y로 가는 비용 을 비교해주는 방식을 반복하면된다.
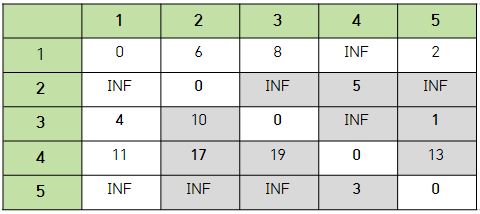
즉, 1을 거쳐서 가는 경우가 더 빠른 경우가 존재한다면 빠른 경우로 최소 비용을 계산한다. 그 결과 다음과 같이 표가 구성된다.
- 노드 1을 거쳐가는 경우 결과 테이블
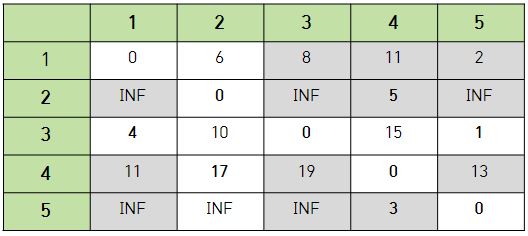
- 노드 2을 거쳐가는 경우 결과 테이블
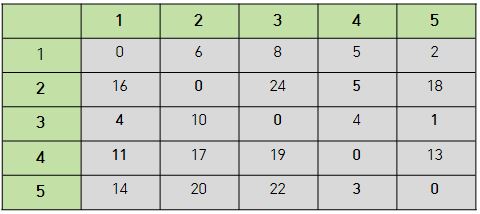
- 노드 3을 거쳐가는 경우 결과 테이블
- 위와 같은 방식으로 노드 4번 5번에 대해서도 수행해주면 다음과 같은 결과가 만들어진다.
Source Code
#include <stdio.h>
int num = 4;
int INF = 10000000;
int a[4][4] = {
{0, 5, INF, 8},
{7, 0, 9, INF},
{2, INF, 0, 4},
{INF, INF, 3, 0},
};
void floydWarshall(){
// 결과 그래프를 초기화 한다.
int d[num][num];
for(int i = 0; i < num; i++){
for(int j = 0; j < num; j++){
d[i][j] = a[i][j];
}
}
// k = 거쳐가는 노드
for(int k = 0; k < num; k++){
// i = 출발 노드
for(int i = 0; i < num; i++){
// j = 도착 노드
for(int j = 0; j < num; j++){
if(d[i][k] + d[k][j] < d[i][j]){
d[i][j] = d[i][k] + d[k][j];
}
}
}
}
// 결과 출력
for(int i = 0; i < num; i++){
for(int j = 0; j < num; j++){
printf("%d ",d[i][j]);
}
printf("\n");
}
}
int main(void){
floydWarshall();
return 0;
}