record
위상 정렬(Topology Sort) 이란?
- ‘순서가 정해져있는 작업’을 차례로 수행해야 할 때 그 순서를 결정해주기 위해 사용하는 알고리즘이다.
- 다음과 같이 순서가 정해져있는 작업의 예시이다.
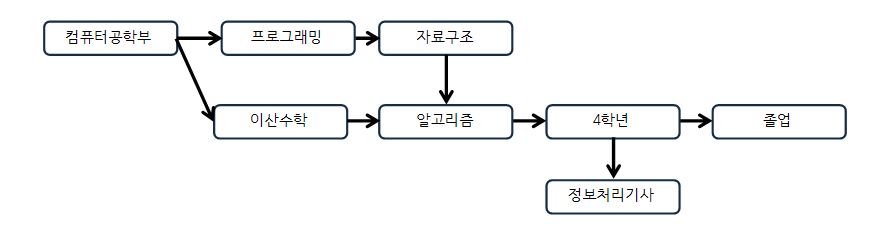
그래프의 흐름을 ‘조건’ 으로 해석할 수 있다. 알고리즘 수업을 이수하기 위해서는 이전에 선 이수 과목인 이산수학과 자료구조를 이수해야만 알고리즘을 수강할 수 있다는 말이다.
-
사이클이 발생하는 경우 에는 위상정렬을 수행할 수 없으므로 주의 해야한다.
-
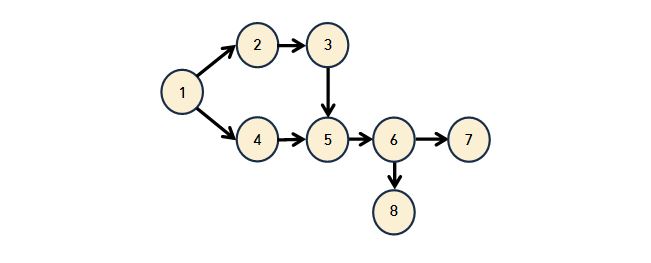
위상정렬 초기 그래프
위의 예시를 그대로 노드에 숫자로 표기한 그래프이다.
위상 정렬(Topology Sort) 알고리즘의 특징
- 위상 정렬(Topology Sort) 은 여러 개의 답이 존재할 수 있다.
- 위상 정렬(Topology Sort) 은 DAG(Directed Acyclic Graph) 에만 적용이 가능하다.
- DAG(Directed Acyclic Graph) 이란, 방향은 존재 하지만 사이클이 발생하지 않는 그래프를 의미한다.
- 사이클이 발생하는 경우 위상 정렬을 수행할 수 없다.!!!!!!
- 이유는 위상 정렬은 시작점이 존재해야 하기 때문이다.
- 위상 정렬(Topology Sort) 을 수행하는 알고리즘으로는 스택(stack), 큐(Queue) 를 이용하여 수행할 수 있다.
위상 정렬(Topology Sort)의 알고리즘 예시
- 큐(Queue) 를 이용하여 위상 정렬 알고리즘 수행 예시
- 진입차수가 0인 정점을 큐에 삽입한다.
- 큐에서 원소를 꺼내 연결된 모든 간선을 제거한다.
- 간선 제거 이후에 진입차수가 0이 된 정점을 큐에 삽입한다.
- 큐가 빌 때 까지 2~3번 과정을 반복한다.
- 모든 원소를 방문하기 전에 큐가 빈다면 사이클이 존재하는 것이다.
-
모든원소를 방문했다면 큐에서 꺼낸 순서가 위상 정렬의 결과이다.
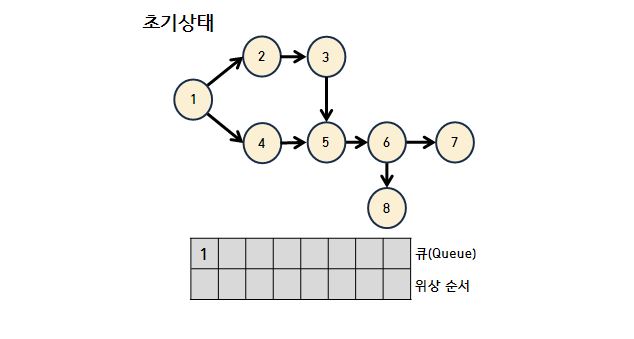
- 초기 상태
위와 같이 처음에는 진입차수가 0인 1번 노드가 큐에 들어가 있다.
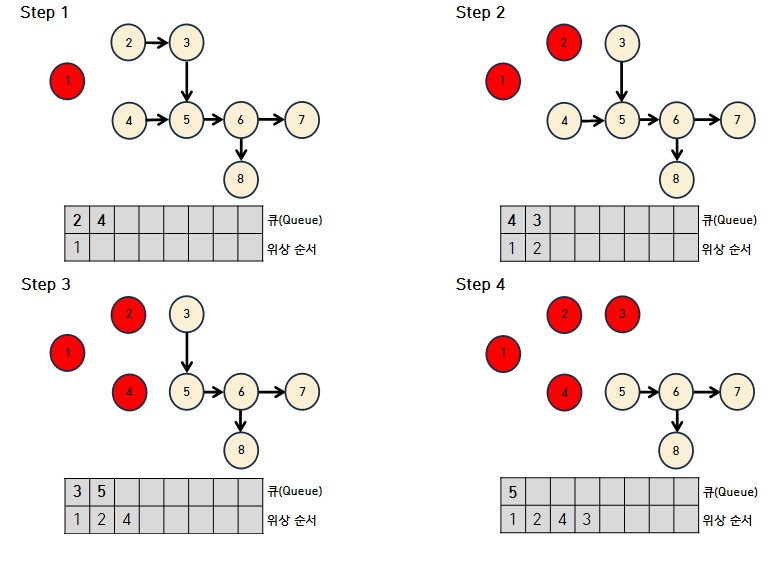
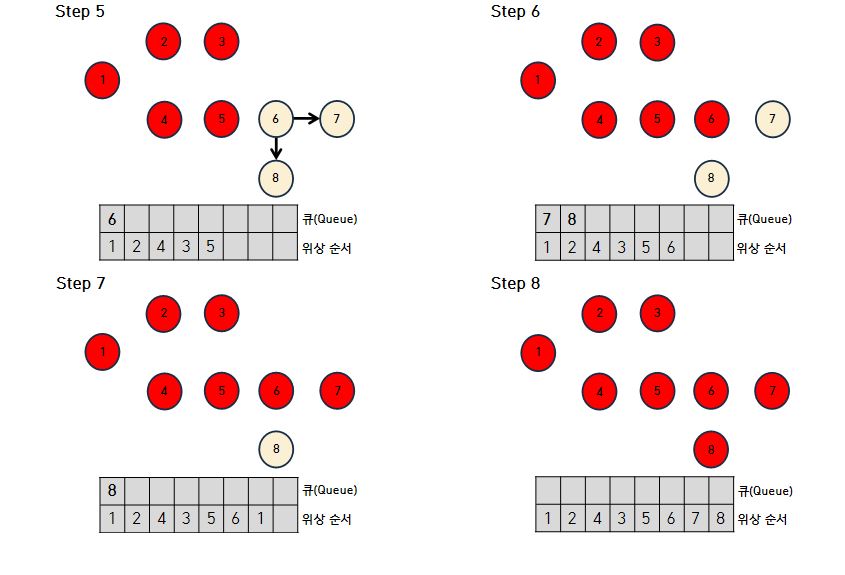
- 진입 차수가 0인 노드를 큐에 삽입하고 큐에서 원소를 꺼내 해당 원소와 연결된 모든 간선을 제거한다. 그리고 간선 제거 이후에 새롭게 진입차수가 0이 된 정점을 큐에 삽입한다.
- 이와 같은 과정을 큐가 빌 때 까지 반복한다.
결과적으로 1 2 4 3 5 6 7 8 순서로 정렬됨을 알 수 있다.
Source Code
#include <iostream>
#include <vector>
#include <queue>
#define MAX 10
using namespace std;
int n, inDegree[MAX];// inDegree: 진입 차수
vector<int> a[MAX]; // 각 정점의 노드의 정보를 담는다.
void topologySort() {
int result[MAX];
queue<int> q;
// 진입 차수가 0인 노드를 큐에 삽입한다.
for(int i = 1; i <= n; i++){
if(inDegree[i] == 0) q.push(i);
}
// 위상 정렬이 완전히 수행되려면 정확히 N개의 노드를 방문한다.
for(int i = 1; i <= n; i++){
// n개를 방문하기 전에 큐가 빈다면 사이클이 발생한 것.
if(q.empty()){
printf("사이클 발생!!");
return;
}
int x = q.front();
q.pop();
result[i] = x;
for(int i = 0; i < a[x].size(); i++){
int y = a[x][i];
// 새롭게 진입차수가 0이 된 정점을 큐에 삽입한다.
if(--inDegree[y] == 0){
q.push(y);
}
}
}
for(int i = 1; i <= n; i++) {
printf("%d ", result[i]);
}
}
int main(void) {
n = 7;
a[1].push_back(2);
inDegree[2]++;
a[1].push_back(5);
inDegree[5]++;
a[2].push_back(3);
inDegree[3]++;
a[3].push_back(4);
inDegree[4]++;
a[4].push_back(6);
inDegree[6]++;
a[5].push_back(6);
inDegree[6]++;
a[6].push_back(7);
inDegree[7]++;
topologySort();
return 0;
}위상 정렬(Topology Sort)의 시간복잡도
위상 정렬 은 정점의 갯수 + 간선의 갯수 만큼 소요되므로 매우 빠른 알고리즘 중 하나이다.
따라서, 시간 복잡도는 O(V + E) 이다.