크루스칼 알고리즘(Kruskal Algorithm) 이란?
- 탐욕적인 방법(greedy method)을 이용하여 네트워크(간선에 가중치를 할당한 그래프)의 모든 정점을 최소 비용 으로 연결하는 최적 해답을 구하는것.
- 가장 적은 비용으로 모든 노드를 연결하기 위해 사용하는 알고리즘, 즉 최소 비용 신장 트리를 만들기 위한 대표적인 알고리즘이다.
- 예를 들어 설명하면, 여러 개의 도시가 있을 때 각 도시를 도로를 이용해 연결 하고자 할 때 비용을 최소한으로 하고자 할 때 실제로 적용되는 알고리즘이다.
크루스칼 알고리즘(Kruskal Algorithm)의 알고리즘 예시
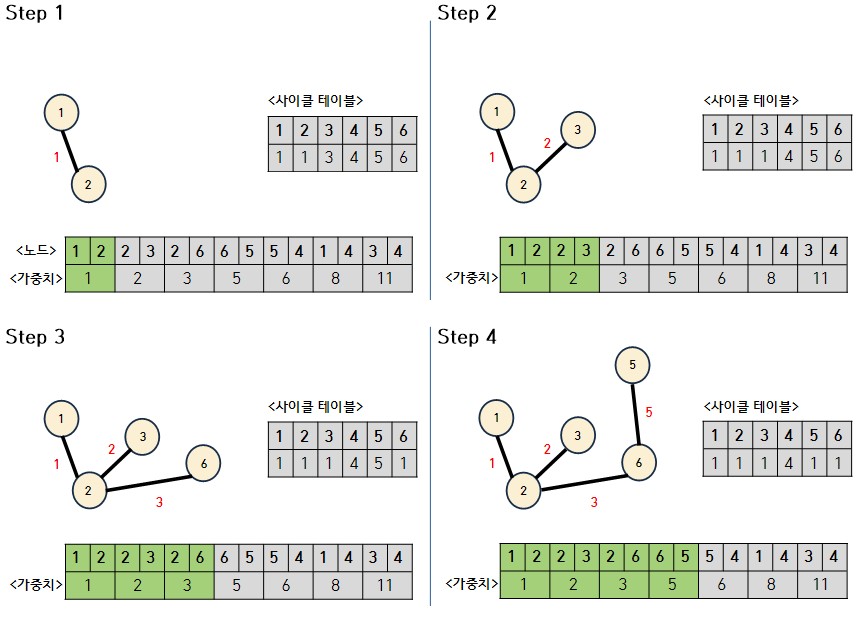
- 최소비용을 선택하기 때문에 오름 차순으로 정렬된 순서에 맞게 그래프에 포함시킨다.
- 포함시키기 전에 사이클 테이블을 확인한다. 사이클 발생 여부는 Union-Find 알고리즘을 적용하여 확인한다.
- 사이클을 형성하는 경우 간선을 포함하지 않는다.
- 가중치를 오름 차순으로 정렬하고 간선을 차례로 하나씩 선택한다.
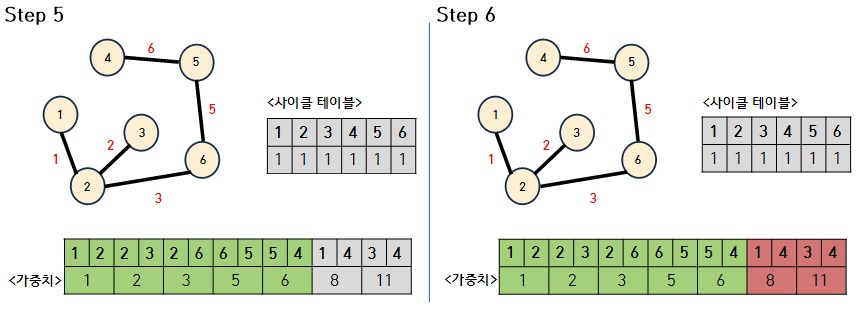
- Step6에서 나머지 간선은 사이클이 형성 되기 때문에 skip 한다.
C++ STL Library를 사용한 크루스칼 알고리즘(Kruskal Algorithm) 구현
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
// 부모 노드를 찾는 함수
int getParent(int parent[], int x) {
if(parent[x] == x) return x;
return parent[x] = getParent(parent, parent[x]);
}
// 두 부모 노드를 합치는 함수
int unionParent(int parent[],int a, int b){
a = getParent(parent, a);
b = getParent(parent, b);
if(a < b) parent[b] = a;
else parent[a] = b;
}
// 같은 부모를 가지는지 확인 == 같은 그래프인지 확인
int findParent(int parent[], int a, int b){
a = getParent(parent, a);
b = getParent(parent, b);
if(a == b) return 1;
return 0;
}
// 간선 선언 클래스
class Edge {
public:
int node[2];
int distance;
Edge(int a, int b, int distance){
this -> node[0] = a;
this -> node[1] = b;
this -> distance = distance;
}
// 거리가 작은 순으로 정렬 기준을 정해준다.
bool operator < (Edge &edge) {
return this->distance < edge.distance;
}
};
int main(void){
int n = 7;
int m = 11;
vector<Edge> v;
// 11개의 간선의 정보
v.push_back(Edge(1, 7, 12));
v.push_back(Edge(1, 4, 28));
v.push_back(Edge(1, 2, 67));
v.push_back(Edge(1, 5, 17));
v.push_back(Edge(2, 4, 24));
v.push_back(Edge(2, 5, 62));
v.push_back(Edge(3, 5, 20));
v.push_back(Edge(3, 6, 37));
v.push_back(Edge(4, 7, 13));
v.push_back(Edge(5, 6, 45));
v.push_back(Edge(5, 7, 73));
// 간선의 비용을 기준으로 오름차순 정렬
sort(v.begin(), v.end());
// 각 정점이 포함된 그래프가 어디인지 저장
int parent[n];
// 각 정점을 자신을 가리키게 초기화하는것 -> Union Find 를 이용하는거다.
for(int i = 0; i < n; i++){
parent[i] = i;
}
int sum = 0;
for(int i = 0; i < v.size(); i++){
// 사이클이 발생하지 않는 경우 그래프에 포함한다.
if(!findParent(parent, v[i].node[0] - 1, v[i].node[1] - 1)){
sum += v[i].distance;
unionParent(parent, v[i].node[0] - 1, v[i].node[1] - 1);
}
}
printf("%d", sum);
return 0;
}크루스칼 알고리즘 은 Union-find 알고리즘을 이용하게 된다면 Kruskal 알고리즘의 시간복잡도는 간선들을 정렬하는 시간에 좌우된다.
즉, 퀵 정렬 과 같은 효율적인 알고리즘으로 정렬을 한다면…크루스칼 알고리즘(Kruskal Algorithm) 의 시간 복잡도는 O(e * log e) 이 된다.