합병 정렬(Merge Sort) 이란?
- 대표적인 ‘분할 정복’ 방법을 채택한 알고리즘이다.
- 우선 반으로 나누고 나중에 합쳐서 정렬하는 알고리즘.
- 퀵 정렬과 동일하게 O(N*logN)의 시간 복잡도를 가진다. 다만 퀵 정렬은 피벗 값에 따라서 편향되게 분할할 가능성이 있다는 점에서 최악의 경우 O(N^2)의 시간 복잡도를 가진다.
- 합병 정렬은 정확히 반절씩 나눈다는 점에서 최악의 경우에도 O(N*logN)을 보장한다.
합병 정렬(Merge Sort) 알고리즘의 특징
- 퀵 정렬보다 빠르지는 않지만 O(N*logN)을 보장할 수 있다는 점에서 강력하다고 할 수 있다.
- 병합한 데이터를 저장하기 위해 추가적인 메모리 사용이 필요 합니다.
- 추가적인 메모리 사용 없는 정렬(in-place sort)에는 힙 정렬 이 있습니다.
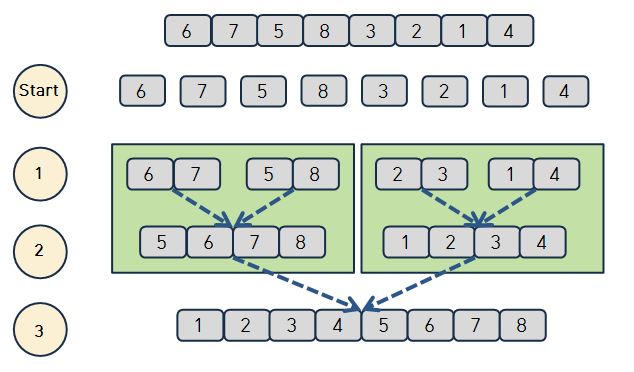
합병 정렬(Merge Sort)의 알고리즘 예시
- 합병 정렬은 퀵 정렬과 다르게 피벗 값이 없고 항상 반으로 나눈다는 특징이 있고 합치는 순간에 정렬을 한다.
바로 이 특징이 단계의 크기가 logN이 되도록 만들어준다.
- 추가적인 메모리 사용 없는 정렬(in-place sort)에는 힙 정렬 이 있습니다.
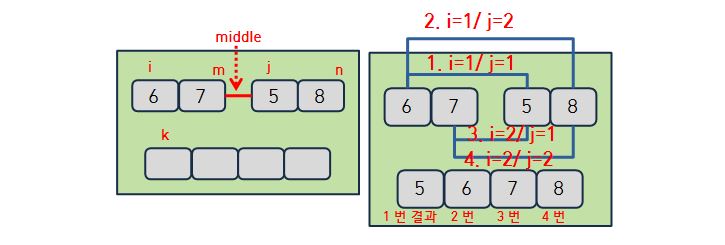
- 단계가 logN이라는 것을 이해했다. 근데 왜 정렬에 필요한 수행시간이 N밖에 되지 않는가? 이유는 다음과 같다.
- 초기 상태는 위와 같다. 왼쪽 집합에서는 i가 첫 번째 원소를 가리키고, 두번째 집합에서는 j가 두번째 원소를 가리킨다. 그리고 정렬된 배열은 비어있는 상태다. 정렬에 N만 걸리는 이유는 삽입 정렬과 동일한 이유다. 바로 ‘부분 집합은 이미 정렬이 되어 있는 상태’ 라고 가정하기 때문이다. 이미 정렬이 되어있는 배열을 합치는 것은 시간 복잡도 O(N)이면 충분 하다.
합병 정렬 구현하기
- C++ 예시1(일반 구현법)
- C++ 예시2(빠른 구현법)
- Java 예시1
C++ 예시1(일반 구현법)
#include <stdio.h>
int num = 8;
int sortedArray[8]; // 정렬 배열은 전역변수로 선언
void mergeSort(int array[], int m, int middle, int n){
int i = m;
int j = middle + 1;
int k = m;
// 오름차순으로 배열에 저장
while(i <= middle && j <= n){
if(array[i] <= array[j]){
sortedArray[k] = array[i];
i++;
} else {
sortedArray[k] = array[j];
j++;
}
k++;
}
// 남은 데이터 저장
if(i > middle){
// i가 먼저 끝났을때 j의 남은 데이터 저장
for(int r = j; r <= n; r++){
sortedArray[k] = array[r];
k++;
}
} else {
// j가 먼저 끝났을때 i의 남은 데이터 저장
for(int r = i; r <= middle; r++){
sortedArray[k] = array[r];
k++;
}
}
// 정렬된 배열 저장
for(int r = m; r <= n; r++){
array[r] = sortedArray[r];
}
}
void divide(int array[], int m, int n){
// 1 보다 큰 경우
if( m < n ){
int middle = ( m + n ) / 2;
divide(array, m, middle); // 왼쪽 분할
divide(array, middle + 1, n); // 오른쪽 분할
mergeSort(array, m, middle, n); // 정렬된 배열 합치기
}
}
int main(void){
int array[num] = {1, 5, 8, 4, 2, 6, 7, 3};
divide(array, 0, num - 1);
for(int i = 0; i < num; i++){
printf("%d ", array[i]);
}
return 0;
}
C++ 예시2(빠른 구현법)
#include <bits/stdc++.h>
using namespace std;
int temp[8];//병합 데이터 임시 저장 배열
void mergeSort(int* arr, int len) {
if(len < 2) return;
int i,j,k;//i 왼쪽, j 오른쪽, k 합병배열 인덱스
int mid = len/2;
i = 0, j = mid, k = 0;
mergeSort(arr, mid);
mergeSort((arr+mid), (len-mid));
while (i < mid && j < len) {//합병
if(arr[i] < arr[j]) {
temp[k++] = arr[i++];
} else {
temp[k++] = arr[j++];
}
}
while (i < mid) {
temp[k++] = arr[i++];
}
while (j < len) {
temp[k++] = arr[j++];
}
//mergeSort의 오버헤드
for (int idx = 0; idx < len; idx++) {
arr[idx] = temp[idx];
}
}
void solve() {
int arr[8] = {6,7,5,8,3,2,1,4};
int size = (sizeof(arr)/sizeof(arr[0]));
cout << "====prev====\n";
for (int i = 0; i < size; i++) {
cout << arr[i] << " ";
}
mergeSort(arr, size);
cout << "\n====after====\n";
for (int i = 0; i < size; i++) {
cout << arr[i] << " ";
}
}
int main(void){
ios::sync_with_stdio(false);
cin.tie(nullptr);
solve();
return 0;
}
Java 구현 예시1
class Main {
static int[] temp;//병합 데이터 임시 배열
public static void mergeSort(int[] arr, int start, int mid, int end) {
int i=start;
int j=mid+1;
int k=start;//i:왼쪽 인덱스, j:오른쪽 인덱스, k:병합 배열 인덱스
while(i <= mid && j <= end) {
if(arr[i] < arr[j]) {
temp[k++] = arr[i++];
} else {
temp[k++] = arr[j++];
}
}
while(i <= mid) {
temp[k++] = arr[i++];
}
while(j <= end) {
temp[k++] = arr[j++];
}
for (int idx = start; idx <= end; idx++) {
arr[idx] = temp[idx];
}
}
public static void divide(int[] arr, int start, int end) {
if(start < end) {
int mid = (start+end)/2;
divide(arr, start, mid);
divide(arr, mid+1, end);
mergeSort(arr, start, mid, end);
}
}
public static void main(String[] args) throws Exception {
int[] arr = {6,7,5,8,3,2,1,4};
temp = new int[arr.length];
//prev
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i] + " ");
}
System.out.println();
divide(arr, 0, arr.length-1);
//result
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i] + " ");
}
}
}
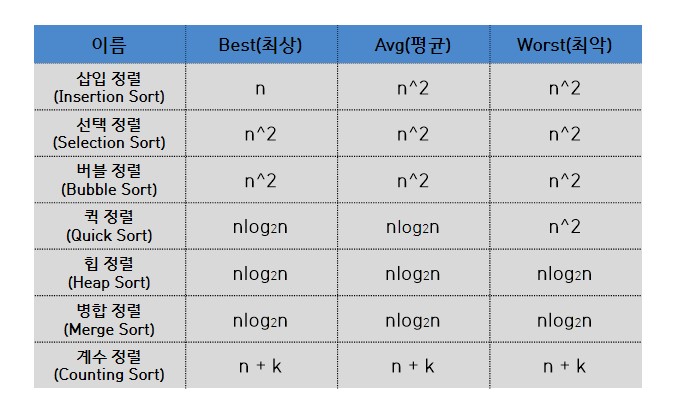
합병 정렬(Merge Sort)의 시간복잡도
합병 정렬의 시간복잡도는 O(N*logN) 이다.